Pembagian Polinomial Satu Variabel  oleh
oleh 
Suatu polinomial satu variabel  jika dibagi
jika dibagi 
maka dapat dinyatakan dalam bentuk berikut
dapat dinyatakan dalam bentuk berikut
maka
Dimana 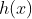 merupakan hasil bagi,
merupakan hasil bagi,  merupakan pembagi dan
merupakan pembagi dan  adalah sisa pembagian
adalah sisa pembagian  oleh
oleh 
Menentukan sisa bagi dari  oleh
oleh  .
.
Untuk menentukan sisa bagi  oleh
oleh  berdasarkan
berdasarkan  , maka cukup menentukan nilai dari p dan q yang merupakan penyelesaian dari sistem persamaan linier dua variabel p dan q.
, maka cukup menentukan nilai dari p dan q yang merupakan penyelesaian dari sistem persamaan linier dua variabel p dan q.



dengan eliminasi atau subtitusi dapat diperoleh
- Membagi
dengan
secara langsung menggunakan pembagian bersusun atau poro-gapit.
- Menggunakan cara Horner bertingkat dengan catatan hasil bagi terakhirnya dibagi dengan a.
Contoh.
1. Tentukan sisa bagi jika  dibagi
dibagi

Pembahasan.
Cara 1
Jika maka
maka 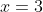 atau
atau 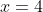
Jika
sehingga diperoleh sistem persamaan linier dua variabel berikut
diperoleh  dan
dan  sehingga sisa pembagiannya adalah
sehingga sisa pembagiannya adalah
 . Dengan cara ini Kita tidak dapat menentukan hasil
. Dengan cara ini Kita tidak dapat menentukan hasil
baginya
baginya
Cara 2
Untuk menentukan sisa pembagian oleh
oleh
 Kita harus menjabarkannya terlebih dahulu menjadi
Kita harus menjabarkannya terlebih dahulu menjadi
bentuk kuadrat yaitu

Untuk menentukan sisa pembagian
bentuk kuadrat yaitu
sehingga sisa pembagiannya adalah  dan hasil baginya
dan hasil baginya
 . Dengan demikian kita dapat menyatakan bahwa
. Dengan demikian kita dapat menyatakan bahwa

Cara 3
Cara ketiga ini menggunakan cara Horner.
Angka 3 pada baris pertama merupakan nilai saat
saat 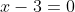 .
.
dimana adalah pembaginya.
adalah pembaginya.
Angka merupakan koefisien dari
merupakan koefisien dari
 mulai dari pangkat tertinggi sampai
mulai dari pangkat tertinggi sampai
terendah.
Langkah 1. Angka 1 jumlahkan diperoleh 1
Langkah 2. hasil langkah 1 kalikan dengan 3 dan letakkan di bawah
angka -1 kemudian jumlahkan diperoleh 2.
Langkah 3. hasil langkah 2 kalikan dengan 3 dan letakkan di bawah
angka -66 kemudian jumlahkan diperoleh -60
Langkah 4. hasil langkah 3 kalikan dengan 3 dan letakkan di bawah
angka 80 kemudian jumlahkan diperoleh -100
Hasil langkah 4 inilah yang dinamakan sisa yaitu -100.
Sampai langkah 4 kita dapat menyatakan

Angka 4 pada baris 3 merupakan nilai saat
saat  . Sedangkan
. Sedangkan
Angka-angka merupakan koefisien hasil bagi
merupakan koefisien hasil bagi  oleh
oleh
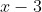 yaitu
yaitu 
Langkah 5. Angka 1 jumlahkan diperoleh 1.
Langkah 6. hasil langkah 5 kalikan dengan 4 dan letakkan di bawah
angka 2 kemudian jumlahkan diperoleh 6.
Langkah 7. hasil langkah 6 kalikan dengan 4 dan letakkan di bawah
angka -60 kemudian jumlahkan diperoleh -36
Sehingga





sehingga sisa pembagiannya adalah  dan hasil baginya
dan hasil baginya
 . Dengan demikian kita dapat menyatakan bahwa
. Dengan demikian kita dapat menyatakan bahwa

Kembali ke Monomial dan polinnomial
Cara ketiga ini menggunakan cara Horner.
Angka 3 pada baris pertama merupakan nilai
dimana
Angka
terendah.
Langkah 1. Angka 1 jumlahkan diperoleh 1
Langkah 2. hasil langkah 1 kalikan dengan 3 dan letakkan di bawah
angka -1 kemudian jumlahkan diperoleh 2.
Langkah 3. hasil langkah 2 kalikan dengan 3 dan letakkan di bawah
angka -66 kemudian jumlahkan diperoleh -60
Langkah 4. hasil langkah 3 kalikan dengan 3 dan letakkan di bawah
angka 80 kemudian jumlahkan diperoleh -100
Hasil langkah 4 inilah yang dinamakan sisa yaitu -100.
Sampai langkah 4 kita dapat menyatakan
Angka 4 pada baris 3 merupakan nilai
Angka-angka
Langkah 5. Angka 1 jumlahkan diperoleh 1.
Langkah 6. hasil langkah 5 kalikan dengan 4 dan letakkan di bawah
angka 2 kemudian jumlahkan diperoleh 6.
Langkah 7. hasil langkah 6 kalikan dengan 4 dan letakkan di bawah
angka -60 kemudian jumlahkan diperoleh -36
Sehingga
Dari cara horner bertingkat diatas dapat dinyatakan dalam bentuk
Kembali ke Monomial dan polinnomial







0 komentar:
Posting Komentar