Organisasi Profesi Guru
bamstheguru di HKSN 2017.
Tema Gambar Slide 2
Deskripsi gambar slide bisa dituliskan disini dengan beberapa kalimat yang menggambarkan gambar slide yang anda pasang, edit slide ini melalui edit HTML template.
Tema Gambar Slide 3
Deskripsi gambar slide bisa dituliskan disini dengan beberapa kalimat yang menggambarkan gambar slide yang anda pasang, edit slide ini melalui edit HTML template.
Tema Gambar Slide 4
bamstheguru pada Mathematics in House Training 3 Jember.
Tema Gambar Slide 5
bamstheguru pada UpGrade Guru KPM.
Diklat Sagusablog Surabaya
Diklat Sagusablog Surabaya Gelombang 1
Selasa, 15 Mei 2018
Selasa, 01 Mei 2018
Penilaian Polinomial 1
Penilaian Polinomial 1 telah dilaksanakan 13 Maret 2018 yang terdiri dari 10 soal
Tes perbaikan pertama dan susulan pertama telah dilaksanakab pada 1 Mei 2018.
Tes perbaikan kedua dan susulan kedua telah dilaksanakan pada 3 Mei 2018
Hasil capaian penilaian tersebut seperti terlihat dalam tabel dibawah ini
Tes perbaikan pertama dan susulan pertama telah dilaksanakab pada 1 Mei 2018.
Tes perbaikan kedua dan susulan kedua telah dilaksanakan pada 3 Mei 2018
Hasil capaian penilaian tersebut seperti terlihat dalam tabel dibawah ini
Senin, 30 April 2018
Penilaian Teorema Sisa dan Teorema Faktor Kelas XI-1 SMAN 7 Surabaya
Alhamdulillah penilaian Teorema Sisa dan Teorema Vaktor telah dilaksanakan di www.onklas.com
Penilaian terdiri dari 8 soal pilihan ganda dengan durasi waktu pengerjaan 60 menit telah dilaksanakan pada 30 April 2018.
Tes perbaikan pertama dan tes susulan pertama telas dilaksanakan tanggal 1 Mei 2018
Tes perbaikan kedua dan tes susulan kedua telah dilaksanakan tanggal 3 Mei 2018
Adapun hasil capaian penilaiannya sebagai berikut
Penilaian terdiri dari 8 soal pilihan ganda dengan durasi waktu pengerjaan 60 menit telah dilaksanakan pada 30 April 2018.
Tes perbaikan pertama dan tes susulan pertama telas dilaksanakan tanggal 1 Mei 2018
Tes perbaikan kedua dan tes susulan kedua telah dilaksanakan tanggal 3 Mei 2018
Adapun hasil capaian penilaiannya sebagai berikut
Kamis, 26 April 2018
Sabtu, 14 April 2018
Jumat, 13 April 2018
Senin, 09 April 2018
Minggu, 08 April 2018
Sabtu, 07 April 2018
Senin, 26 Maret 2018
Nilai maksimum fungsi $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$
Nilai maksimum fungsi $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ adalah ...
Pembahasan
Untuk menentukan nilai maksimum suatu fungsi perlu memperhatikan beberapa hal berikut:
Adapun gambar yang terbentuk sebagai berikut
Dari gambar terlihat jelas bahwa nilai maksimum $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ adalah 4.
Lalu bagaimana jika kita kesulitan menggambarkan grafik fungsinya?
Tenang, itu bukalah permasalahan yang sulit.
kali ini saya akan menggunakan karakteristik dari $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$
Perhatikan syarat-syarat $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ terdefinisi:
Pembahasan
Untuk menentukan nilai maksimum suatu fungsi perlu memperhatikan beberapa hal berikut:
- Jika tahu grafik fungsinya maka dengan mudah dapat ditentukan. Namun untuk urusan mengambar grafik ini bukanlah perkara mudah bagi kebanyakan orang.
- Karakteristik dari fungsi yang sedang ditentukan
- Menggunakan karakteristik stationer suatu fungsi
Adapun gambar yang terbentuk sebagai berikut
 |
| Gambar 1. $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ |
Dari gambar terlihat jelas bahwa nilai maksimum $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ adalah 4.
Lalu bagaimana jika kita kesulitan menggambarkan grafik fungsinya?
Tenang, itu bukalah permasalahan yang sulit.
kali ini saya akan menggunakan karakteristik dari $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$
Perhatikan syarat-syarat $f(x)=\log_{2} (x+5)+\log_{2} (3-x)$ terdefinisi:
- x+5>0 atau x>-5
- 3-x>0 atau x<3
Minggu, 25 Maret 2018
Simulasi Menentukkan Sudut Segitiga Jika Diketahui Panjang Ketiga Sisinya dengan GeoGebra
GeoGebra merupakan aplikasi DINAMIS & GRATIS yang dapat digunakan untuk memudahkan dalam memahami Aljabar, Geometri , Kalkulator Grafik 2D/3D dan CAS.
Berikut adalah contoh salah satu Aplet GeoGebra yang saya gunakan untuk mensimulasikan cara menentukan sudut segitiga jika diketahui panjang ketiga sisinya.
Aplet ini juga memfasilitasi pengguna untuk mengubah ukuran dari ketiga sisi segitiga.
Untuk mengoperasikannya silakan geser titik warna Merah, Hijau dan Biru untuk mengubah ukuran sisi sisi segitiga ABC
Adapun titik dengan label halaman digunakan untuk pindah lembar kerja, sedangkan titik dengan label langkah digunakan mengetahui urutan perhitungan atau penyelesaian tiap halaman
Selamat menikmati
Berikut adalah contoh salah satu Aplet GeoGebra yang saya gunakan untuk mensimulasikan cara menentukan sudut segitiga jika diketahui panjang ketiga sisinya.
Aplet ini juga memfasilitasi pengguna untuk mengubah ukuran dari ketiga sisi segitiga.
Untuk mengoperasikannya silakan geser titik warna Merah, Hijau dan Biru untuk mengubah ukuran sisi sisi segitiga ABC
Adapun titik dengan label halaman digunakan untuk pindah lembar kerja, sedangkan titik dengan label langkah digunakan mengetahui urutan perhitungan atau penyelesaian tiap halaman
Selamat menikmati
Remedial Kelas 12-1
Untuk anak-anakku yang hendak memperbaiki nilai ulangan silakan buka www.onklas.com
pilih ujian hari ini, Ahad, 1 April 2018
Adapun tokennya adalah 241344
pilih ujian hari ini, Ahad, 1 April 2018
Adapun tokennya adalah 241344
Sabtu, 24 Maret 2018
Pembahasan Soal Limit Fungsi 1
Nilai dari $\lim _{x\rightarrow \infty }(x^3\sin \frac{1}{x}+x)(\frac{1}{x-1}-\frac{1}{x+1})=\cdots$
Pembahasan
$\lim _{x\rightarrow \infty }(x^3\sin \frac{1}{x}+x)(\frac{1}{x-1}-\frac{1}{x+1})=L$
Permasalahan diatas harus kita bawa ke bentuk berikut
$\lim_{x\rightarrow 0} \frac{\sin nx}{nx}=\lim_{x \rightarrow 0} \frac{nx}{\sin nx}=1$
atau
$\lim_{x\rightarrow \infty} \frac{\sin \frac{1}{nx}}{\frac{1}{nx}}=\lim_{x \rightarrow \infty} \frac{\frac{1}{nx}}{\sin \frac{1}{nx}}=1$
atau
$\lim_{x\rightarrow \infty} nx \sin \frac{1}{nx}=\lim_{x \rightarrow \infty} \frac{1}{nx\sin \frac{1}{nx}}=1$
Mari Kita proses
misalkan $p=\frac{1}{x}$ dan $x\rightarrow \infty$ maka $p\rightarrow 0$
Dengan demikian soal diatas dapat kita tuliskan menjadi
$L=\lim _{p\rightarrow 0 }(\frac{1}{p^3}\sin p +\frac{1}{p})(\frac{1}{\frac{1}{p}-1}-\frac{1}{\frac{1}{p}+1})$
$L=\lim _{p\rightarrow 0 }(\frac{1}{p^2}\frac{\sin p}{p} +\frac{1}{p})(\frac{p}{1-p}-\frac{p}{1+p})$
$L=\lim _{p\rightarrow 0 }(\frac{1}{p^2}+\frac{1}{p})(\frac{2p^2}{1-p^2})$
$L=\lim _{p\rightarrow 0 }(\frac{1+p}{p^2})(\frac{2p^2}{1-p^2})$
$L=\lim _{p\rightarrow 0 }\frac{2(1+p)}{1-p^2}$
$L=\lim _{p\rightarrow 0 }\frac{2}{1-p}$
$L=2$
Jumat, 23 Maret 2018
Pembahasan Soal Bilangan Berpangkat dan Pemfaktoran 1
Nilai dari $\frac{2017\cdot (2016^2-16)\cdot 2015}{2020\cdot (2016^2-1)}=\cdots$
A. 2012
B. 2013
C. 2014
D. 2015
Penyelesaian A
$\frac{2017\cdot (2016^2-16)\cdot 2015}{2020\cdot (2016^2-1)}= K$
Mari kita faktorkan
$K=\frac{2017 \cdot (2016-4)\cdot (2016+4) \cdot 2015}{2020\cdot (2016-1)\cdot (2016+1)}$
Mari kita sederhanakan
$K=\frac{2017 \cdot 2012\cdot 2020 \cdot 2015}{2020\cdot 2015 \cdot 2017}$
Sehingga
$K=2012$
A. 2012
B. 2013
C. 2014
D. 2015
Penyelesaian A
$\frac{2017\cdot (2016^2-16)\cdot 2015}{2020\cdot (2016^2-1)}= K$
Mari kita faktorkan
$K=\frac{2017 \cdot (2016-4)\cdot (2016+4) \cdot 2015}{2020\cdot (2016-1)\cdot (2016+1)}$
Mari kita sederhanakan
$K=\frac{2017 \cdot 2012\cdot 2020 \cdot 2015}{2020\cdot 2015 \cdot 2017}$
Sehingga
$K=2012$
Senin, 19 Maret 2018
Penyederhanaan Polinomial 1
$(5+6)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=6^x-5^y$. Berapakah nilai $x+y=\cdots$
Pembahasan
$(5+6)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6-5)(5+6)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=(6-5)L$
$(6^2-5^2)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^4-5^4)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^8-5^8)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^{16}-5^{16})(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^{32}-5^{32})(5^{32}+6^{32})=L$
$(6^{64}-5^{64})=L=6^x-5^y$
Sehingga $ x+y=64+64=128$
Jadi nilai $ x+y=128 $
Pembahasan
$(5+6)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6-5)(5+6)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=(6-5)L$
$(6^2-5^2)(5^2+6^2)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^4-5^4)(5^4+6^4)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^8-5^8)(5^8+6^8)(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^{16}-5^{16})(5^{16}+6^{16})(5^{32}+6^{32})=L$
$(6^{32}-5^{32})(5^{32}+6^{32})=L$
$(6^{64}-5^{64})=L=6^x-5^y$
Sehingga $ x+y=64+64=128$
Jadi nilai $ x+y=128 $
Pembahasan barisan dan deret 4
Jika $1^2+2^2+3^2+4^2+5^2+\cdots+50^2=X$. Berapakah $2^2+4^2+6^2+8^2+10^2+\cdots+100^2=\cdots$
Pembahasan
$1^2+2^2+3^2+4^2+5^2+\cdots+50^2=X$
$2^2+4^2+6^2+8^2+10^2+\cdots+100^2=\cdots$
$2^2+4^2+6^2+8^2+10^2+\cdots+100^2=2^2(1^2+2^2+3^2+4^2+5^2+\cdots+50^2)=4X$
Jadi jika $1^2+2^2+3^2+4^2+5^2+\cdots+50^2=X$ maka $2^2+4^2+6^2+8^2+10^2+\cdots+100^2=4X$
Pembahasan
$1^2+2^2+3^2+4^2+5^2+\cdots+50^2=X$
$2^2+4^2+6^2+8^2+10^2+\cdots+100^2=\cdots$
$2^2+4^2+6^2+8^2+10^2+\cdots+100^2=2^2(1^2+2^2+3^2+4^2+5^2+\cdots+50^2)=4X$
Jadi jika $1^2+2^2+3^2+4^2+5^2+\cdots+50^2=X$ maka $2^2+4^2+6^2+8^2+10^2+\cdots+100^2=4X$
Pembahasan Pre Tes OGN Mat Kota Malang 2018 Bagian Kompetensi Profesional No 3
Sisi-sisi suatu dadu menampilkan bilangan $-3,\;-2,\;-1$, 0, 1, 2. Jika Nufail melemparkan dadu tersebut dua kali kemudian mengalikan kedua bilangan yang dihasilkan maka peluang hasil kalinya negatif adalah ....
Pembahasan
Mari kita buat tabel kemungkinan kejadian yang mungkin
Terlihat jelas hasil kali kedua bilangan yang negatif (warna merah) ada 12 kejadian. Sehingga peluang hasil kali kedua bilangan hasil dua kali pelemparan dadu yang hasil kalinya negatif adalah $\frac{12}{36}=\frac{1}{3}$
jadi peluang hasil kali kedua bilangan hasil dua kali pelemparan dadu yang hasil kalinya negatif adalah $\frac{1}{3}$
Minggu, 18 Maret 2018
Pembahasan Soal Keterbagian Bilangan Bulat 1
Sebuah bilangan sepuluh digit $2018a2018b$ habis dibagi 36. Jumlah semua nilai $a$ dan $b$ yang mungkin adalah ....
Pembahasan
Bilangan $2018a2018b$ habis dibagi 36 berarti $2018a2018b$ habis dibagi 4 dan 9.
Jika $2018a2018b$ habis dibagi 4 maka $8b$ habis dibagi 4. dengan kata lain nilai $b$ yang mungkin adalah 0, 4, dan 8.
Jika $2018a2018b$ habis dibagi 9 maka $2+0+1+8+a+2+0+1+8+b$ habis dibagi 9 dengan kata lain $4+a+b$ habis dibagi 9. Hal ini memunculkan dua kemungkinan nilai $a+b$ yaitu 5 atau 14.
Mari kita data
Jika $b=0$ maka nilai $a$ yang mungkin adalah 5.
Jika $b=4$ maka nilai $a$ yang mungkin adalah 1.
Jika $b=8$ maka nilai $a$ yang mungkin adalah 6.
Sehingga jumlah nilai $a$ dan $b$ yang mungkin adalah $0+5+1+4+8+6=24$
Jadi jumlah nilai $a$ dan $b$ yang mungkin adalah 24.
Pembahasan Pre Tes OGN Mat Kota Malang 2018 Bagian Kompetensi Profesional No 2
 |
| Gambar 1. Soal aslinya |
Dalam persegi panjang $ABCD$ yang ditunjukkan gambar 1 di atas, $M_1$ adalah titik tengah dari $DC$, $M_2$ adalah titik tengah dari $AM_1$. $M_3$ adalah titik tengah $BM_2$. dan $M_4$ adalah titik tengah $CM_3$. Perbandingan luas dari segiempat $M_1M_2M_3M_4$ dan persegi panjang $ABCD$ adalah ....
Pembahasan
 |
| Gambar 2 Penjelas |
Misalkan $AB=2y$ dan $AD=2x$
$\Delta AM_1D$ sebagun dengan $\Delta AEM_2$ sehingga
$\frac{EM_2}{AD}=\frac{AM_2}{AM_1}=\frac{1}{2} \rightarrow EM_2=\frac{1}{2}AD=x$.
$\frac{AE}{DM_1}=\frac{AM_2}{AM_1}=\frac{1}{2} \rightarrow AE=\frac{1}{2}DM_1=\frac{1}{2}y$.
Jika $AE=\frac{1}{2}y$ dan $\Delta BM_2E$ sebagun dengan $\Delta M_3BF$ sehingga
$\frac{FM_3}{BE}=\frac{BM_3}{BM_2}=\frac{1}{2} \rightarrow FM_3=\frac{1}{2}BE=\frac{3}{4}y$.
$\frac{FB}{EM_2}=\frac{BM_3}{BM_2}=\frac{1}{2} \rightarrow FB=\frac{1}{2}M_2E=\frac{1}{2}x$.
Jika $BF=\frac{1}{2}x$ dan $\Delta CFM_3$ sebagun dengan $\Delta M_4GC$ sehingga
$\frac{M_4G}{CF}=\frac{CM_4}{CM_3}=\frac{1}{2} \rightarrow M_4G=\frac{1}{2}CF=\frac{3}{4}x$.
$L_{M_1M_2M_3M_4}=L_{ABCD}-(L_{AM_1D}+L_{ABM_2}+L_{BCM_3}+L_{CM_1M_4})$
$L_{M_1M_2M_3M_4}=AB\times AD-(\frac{1}{2}\times AD\times DM_1+\frac{1}{2}\times AB\times EM_2+\frac{1}{2}\times BC\times FM_3+\frac{1}{2}\times CM_1\times GM_4)$
$L_{M_1M_2M_3M_4}=4xy-(xy+xy+\frac{3}{4}xy+\frac{3}{8}xy)=\frac{7}{8}xy$
Sehingga $\frac{L_{M_1M_2M_3M_4}}{L_{ABCD}}=\frac{\frac{7}{8}xy}{4xy}=\frac{7}{32}$
Jadi $\frac{L_{M_1M_2M_3M_4}}{L_{ABCD}}=\frac{7}{32}$
Pembahasan Soal Barisan dan Deret 3
Pada suatu hari Raja memanggil Abu Nawas untuk dites kemampuannya. Di hadapan Abu Nawas ada 10 orang yang masing2 membawa 10 buah timun. Kecuali 1 orang, 9 orang lainnya membawa 10 timun yang beratnya masing2 10 gram sedangkan 1 orang lagi membawa 10 timun yang masing2 beratnya 9 gram. Raja menyerahkan sebuah timbangan kepada Abu Nawas. Timbangan tersebut sejenis timbangan angka. Kalau ditaruh 10 buah timun yang masing 10 gram di timbangan maka angka yang muncul 100 gram. Jika ditaruh 35 buah timun yang masing 10 gram di timbangan maka angka yang muncul 350 gram. Raja meminta Abu Nawas untuk menemukan orang yang membawa 10 timun yang beratnya masing2 9 gram hanya dengan sekali menimbang. Dapatkah Abu Nawas melaksanakan perintah Raja ? Berikan penjelasan..
Pembahasan
Ide Miftahus Saidin
Misalkan sebut saja kesepuluh orang itu A1, A2, A3, ... , A10.
ambil 1 timun di A1
ambil 2 timun di A2
ambil 3 timun di A3
...
...
...
ambil 10 timun di A10
Kemudian ditimbang.
Pada kondisi ini,
Seharusnya klu ke 10 orang membawa timun yg beratnya masing sama, yaitu 10 g maka ditimbangan akan menunjukkan angka 550 g.
Nah jika angka ditimbangan menunjukkan
549 = 550-1 berarti A1 lah orang dimaksud
548 = 550-2 berarti A2 lah orang dimaksud
Dst..
540=550-10 berarti A10 lah orang yg di maksud
Pembahasan Soal Vektor 4
Diketahui $|\vec{u}|$ dan $|\vec{v}|$. Jika $|\vec{u}|=12$, $|\vec{v}|=15$ dan $|\vec{u}+\vec{v}|=24$ maka nilai $|\vec{u}-\vec{v}|=\cdots$
A. $\sqrt{396}$
B. $\sqrt{216}$
C. $\sqrt{207}$
D. $\sqrt{162}$
E. $9$
Pembahasan D
$|\vec{u}|=12$, $|\vec{v}|=15$ dan $|\vec{u}+\vec{v}|=24$
misalkan sudut yang dibentuk oleh $\vec{u}$ dan $\vec{v} $ adalah $ \theta$
$|\vec{u}-\vec{v}|=\cdots$
Ingat!
$|\vec{u}+\vec{v}|^2=|\vec{u}|^2+|\vec{v}|^2+2|\vec{u}||\vec{v}|\cos \theta$
dan
$|\vec{u}-\vec{v}|^2=|\vec{u}|^2+|\vec{v}|^2-2|\vec{u}||\vec{v}|\cos \theta$
sehingga
$|\vec{u}+\vec{v}|^2+|\vec{u}-\vec{v}|^2=2(|\vec{u}|^2+|\vec{v}|^2)$
$24^2+|\vec{u}-\vec{v}|^2=2(12^2+15^2)$
$576+|\vec{u}-\vec{v}|^2=2(144+225)$
$|\vec{u}-\vec{v}|^2=738-576=162$
$|\vec{u}-\vec{v}|=\sqrt{162}$
jadi jika $|\vec{u}|=12$, $|\vec{v}|=15$ dan $|\vec{u}+\vec{v}|=24$ maka nilai $|\vec{u}-\vec{v}|=\sqrt{162}$.
Pembahasan Soal Vektor 3
Diketahui $|\vec{a}|$, $|\vec{b}|$, dan $|\vec{a}-\vec{b}|$ berturut-turut adalah 4, 6, dan $2\sqrt{19}$. Nilai $|\vec{a}+\vec{b}|=\cdots$
A. $4\sqrt{19}$
B. $\sqrt{19}$
C. $4\sqrt{7}$
D. $2\sqrt{7}$
E. $\frac{1}{2}\sqrt{7}$
Pembahasan D
$|\vec{a}|=4$, $|\vec{b}|=6$, dan $|\vec{a}-\vec{b}|=2\sqrt{19}$
misalkan sudut yang dibentuk oleh $\vec{a}$ dan $\vec{b} $ adalah $ \theta$
$|\vec{a}+\vec{b}|=\cdots$
Ingat!
$|\vec{a}+\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2+2|\vec{a}||\vec{b}|\cos \theta$
dan
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos \theta$
sehingga
$|\vec{a}+\vec{b}|^2+|\vec{a}-\vec{b}|^2=2(|\vec{a}|^2+|\vec{b}|^2)$
$|\vec{a}+\vec{b}|^2+(2\sqrt{19})^2=2(4^2+6^2)$
$|\vec{a}+\vec{b}|^2+76=2(16+36)$
$|\vec{a}+\vec{b}|^2=104-76=28$
$|\vec{a}+\vec{b}|=\sqrt{28}=2\sqrt{7}$
$|\vec{a}+\vec{b}|=2\sqrt{7}$
jadi jika $|\vec{a}|$, $|\vec{b}|$, dan $|\vec{a}-\vec{b}|$ berturut-turut adalah 4, 6, dan $2\sqrt{19}$ maka $|\vec{a}+\vec{b}|=2\sqrt{7}$.
Pembahasan Soal Vektor 2
Diketahui vektor $\vec{a}= \begin{pmatrix}1 \\0 \\1 \end{pmatrix}$, $\vec{b}=\begin{pmatrix}x \\ 3\\4 \end{pmatrix}$ dan $\vec{c}=\begin{pmatrix}2 \\1 \\3 \end{pmatrix}$. Jika $(\vec{a}-\vec{b})\cdot \vec{c}=\vec{c} \cdot \vec{a}$, nilai $x$ adalah ....
A. $-8$
B. $-7 \frac{1}{2}$
C. $-3$
D. $3 \frac{1}{2}$
E. 4
Pembahasan B
Jadi nilai $x$ yang memenuhi adalah $-7\frac{1}{2}$
A. $-8$
B. $-7 \frac{1}{2}$
C. $-3$
D. $3 \frac{1}{2}$
E. 4
Pembahasan B
$\vec{a}= \begin{pmatrix}1 \\0 \\1 \end{pmatrix}$ $\vec{b}=\begin{pmatrix}x \\ 3\\4 \end{pmatrix}$ $\vec{c}=\begin{pmatrix}2 \\1 \\3 \end{pmatrix}$
$(\vec{a}-\vec{b})\cdot \vec{c}=\vec{c} \cdot \vec{a}$
$(\begin{pmatrix}1 \\0 \\1 \end{pmatrix}-\begin{pmatrix}x \\ 3\\4 \end{pmatrix})\cdot \begin{pmatrix}2 \\1 \\3 \end{pmatrix}=\begin{pmatrix}2 \\1 \\3 \end{pmatrix} \cdot \begin{pmatrix}1 \\0 \\1 \end{pmatrix}$
$\begin{pmatrix}1-x \\-3 \\-3 \end{pmatrix}\cdot \begin{pmatrix}2 \\1 \\3 \end{pmatrix}=2+0+3$
$2(1-x)-3-9=5$
$-2x-10=5$
$-2x=15$
$x=\frac{15}{-2}=-7\frac{1}{2}$
Jadi nilai $x$ yang memenuhi adalah $-7\frac{1}{2}$
Pembahasan Pre Tes OGN Mat Kota Malang 2018 Bagian Kompetensi Profesional No 1
Diberikan lima bilangan bulat positif $a,\;b, \;c,\;d,\; e$ dan diketahui $c:e=b,\;a+b=d$ dan $e-d=a$. Dari kelima bilangan tersebut, bilangan yang terbesar adalah ....
Pembahasan
$a,\;b, \;c,\;d,\; e$ bilangan bulat positif.
$c:e=\frac{c}{e}=b \rightarrow c=be \rightarrow c>b,e$
$a+b=d \rightarrow d>a,b$
$e-d=a \rightarrow e=a+d \rightarrow e>a,d$
Karena $c>b,e;\;d>a,b;\;e>a,d$ maka $c>a,\;b,\;d,\;e $
Dengan demikian bilangan yang terbesar adalah c
Pembahasan Soal Barisan dan Deret 2
Suatu barisan aritmatika memiliki suku kedua 8, suku keempat adalah 14 dan suku terakhir 23. Jumlah semua suku barisan tersebut adalah ....
Pembahasan C
Diketahui barisan aritmatika.
$u_2=a+b=8$
$u_4=a+3b=14$
$u_n=a+(n-1)b=23$
Ditanyakan $S_n$
$S_n=\frac{n}{2}(a+U_n)$
$\left\{\begin{matrix}a+b=8\\ a+3b=14\end{matrix}\right. $
dengan eliminasi diperoleh $2b=6 \rightarrow b=3$ dan $a=5$
Selanjutnya kita mengidentifikasi berapa nilai $n$?
Jika $u_n=5+(n-1)3=23$ maka $3(n-1)=18 \rightarrow n-1=6 \rightarrow n=7$
Dengan demikian $S_7=\frac{7}{2}(5+23)=98$
Jadi jumlah semua suku barisan tersebut adalah 98.
Teorema Sisa 2 Jika $P(x)$ polinomial berderajat $n$ dibagi $(kx-h)$ maka sisa pembagiannya adalah $S(\frac{h}{k})=P(\frac{h}{k})$
Suatu polinomial dapat dinyatakan dalam bentuk berikut
$ P(x)=a_1x^n+a_2x^{n-1}+a_3x^{n-2}+\cdots+a_{n-2}x^2+a_{n-1}x+a_n $
Jika $P(x)$ dibagi $Q(x)$ memperoleh hasil bagi $H(x)$ dan sisa baginya $S(x)$ maka polinomial tersebut dapat dinyatakan dalam bentuk $ P(x)=H(x)\timesQ(x)+S(x) $
Dimana jika $P(x)$ polinomial berderajat $n$, $Q(x)$ polinomial berderajat $m$, dan $m\leqslant n$ maka polinomial $H(x)$ berderajat $n-m$ dan $S(x)$ berderajat $m-1$.
Teorema Sisa 2
Jika $P(x)$ polinomial berderajat $n$ dibagi $(kx-h)$ maka sisa pembagiannya adalah $S(\frac{h}{k})=P(\frac{h}{k})$
Pembuktian
Perhatikan $P(x)=H(x)(kx-h)+S(x)$ dengan mensubtitusikan $x=\frac{h}{k}$ atau $kx-h=0$ diperoleh
$ P(\frac{h}{k})=H(\frac{h}{k})(k\times \frac{h}{k}-h)+S(\frac{h}{k})$
$ P(\frac{h}{k})=H(\frac{h}{k})\times 0 + S(\frac{h}{k})$
$ P(\frac{h}{k})=0+S(\frac{h}{k})$
$ P(\frac{h}{k})=S(\frac{h}{k})$
Terbukti.
$ P(x)=a_1x^n+a_2x^{n-1}+a_3x^{n-2}+\cdots+a_{n-2}x^2+a_{n-1}x+a_n $
Jika $P(x)$ dibagi $Q(x)$ memperoleh hasil bagi $H(x)$ dan sisa baginya $S(x)$ maka polinomial tersebut dapat dinyatakan dalam bentuk $ P(x)=H(x)\timesQ(x)+S(x) $
Dimana jika $P(x)$ polinomial berderajat $n$, $Q(x)$ polinomial berderajat $m$, dan $m\leqslant n$ maka polinomial $H(x)$ berderajat $n-m$ dan $S(x)$ berderajat $m-1$.
Teorema Sisa 2
Jika $P(x)$ polinomial berderajat $n$ dibagi $(kx-h)$ maka sisa pembagiannya adalah $S(\frac{h}{k})=P(\frac{h}{k})$
Pembuktian
Perhatikan $P(x)=H(x)(kx-h)+S(x)$ dengan mensubtitusikan $x=\frac{h}{k}$ atau $kx-h=0$ diperoleh
$ P(\frac{h}{k})=H(\frac{h}{k})(k\times \frac{h}{k}-h)+S(\frac{h}{k})$
$ P(\frac{h}{k})=H(\frac{h}{k})\times 0 + S(\frac{h}{k})$
$ P(\frac{h}{k})=0+S(\frac{h}{k})$
$ P(\frac{h}{k})=S(\frac{h}{k})$
Terbukti.
Teorema Sisa Jika $P(x)$ polinomial berderajat $n$ dibagi $(x-h)$ maka sisa pembagiannya adalah $S(h)=P(h)$
Suatu polinomial dapat dinyatakan dalam bentuk berikut
Jika $P(x)$ dibagi $Q(x)$ memperoleh hasil bagi $H(x)$ dan sisa baginya $S(x)$ maka polinomial tersebut dapat dinyatakan dalam bentuk
Dimana jika $P(x)$ polinomial berderajat $n$, $Q(x)$ polinomial berderajat $m$, dan $m\leqslant n$ maka polinomial $H(x)$ berderajat $n-m$ dan $S(x)$ berderajat $m-1$.
Teorema Sisa 1
Jika $P(x)$ polinomial berderajat $n$ dibagi $(x-h)$ maka sisa pembagiannya adalah $S(h)=P(h)$
$P(x)=a_1x^n+a_2x^{n-1}+a_3x^{n-2}+\cdots+a_{n-2}x^2+a_{n-1}x+a_n$
Jika $P(x)$ dibagi $Q(x)$ memperoleh hasil bagi $H(x)$ dan sisa baginya $S(x)$ maka polinomial tersebut dapat dinyatakan dalam bentuk
$P(x)=H(x)\timesQ(x)+S(x)$
Dimana jika $P(x)$ polinomial berderajat $n$, $Q(x)$ polinomial berderajat $m$, dan $m\leqslant n$ maka polinomial $H(x)$ berderajat $n-m$ dan $S(x)$ berderajat $m-1$.
Teorema Sisa 1
Jika $P(x)$ polinomial berderajat $n$ dibagi $(x-h)$ maka sisa pembagiannya adalah $S(h)=P(h)$
Sabtu, 17 Maret 2018
Pembagian Suku Banyak dengan Pembagi $ ax^2+bx+c $
PEMBAGIAN SUKU BANYAK DENGAN PEMBAGI $ ax^2+bx+c $
Pembagian suku banyak $ a_1x^n+a_2x^{n-1}+\cdots+a_{n-1}x+a_n $ oleh $ ax^2+bx+c $ dapat dilakukan secara langsung dengan cara Horner-Kino. Untuk mempelajari dan memahami cara Horner-Kino perhatikan contoh berikut.
Pembahasan Soal Deret 1
Dalam menyelesaikan permasalahan deret memang suatu tantangan tersediri. Sebelum kita menentukan nilai suatu deret ada baiknya jika mengamati dan mencermati pola deret yang sedang dihadapi.
Berikut adalah permasalahan menentukan nilai deret yang memuat bilangan faktorial didalamnya. Oleh karenanya perlu kejelian dan ketelitian yang bagus.
Pola deret diatas adalah
Sehingga 
Dengan demikian
Berarti
Pembahasan Soal Fungsi Kuadrat 1
By bamstheguru13.50bamstheguru, Fungsi, Kuadrat, Pembahasan Soal Fungsi Kuadrat, tanya jawab, tryout, unbk, USBNNo comments

Jika fungsi kuadrat f memiliki sifat-sifat
Pembahasan B
Jika
Jika
Dengan demikian
Jika
Jadi jika fungsi kuadrat f memiliki sifat-sifat
Rabu, 14 Maret 2018
Pembahasan Soal Vektor 1
Diketahui vektor
Pembahasan A
Untuk menentukan luas segitiga yang dibentuk oleh vektor
Untuk menentukan luas segitiga yang dibentuk oleh vektor  dan
dan 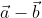 kita menggunakan rumus
kita menggunakan rumus
Sehingga perbandingan luas segitiga yang dibentuk oleh vektor 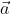 dan
dan 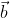 dengan luas segitiga yang dibentuk
dengan luas segitiga yang dibentuk  dan
dan 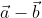 adalah
adalah